THE LAW OF SYMMETRY
It states that all crystals of a substance possess the same elements of symmetry. The three important elements of symmetry are:
(i) plane of symmetry,
(ii) axis of symmetry,
(iii) centre of symmetry.
(A) Plane of Symmetry
It is an imaginary plane which can divide the crystal into two halves such that one is the mirror image of the other. A cubic crystal, for example, has two types of plane of symmetry.
(i) Rectangular planes of symmetry: These are the planes situated midway and parallel to the opposite faces. Since a cubic crystal has six faces, i.e. three pairs of opposite faces, it has three rectangular plane of symmetry as shown in following figure (a).
(ii) Diagonal plane of symmetry: These are the plane touching the opposite edges. As they lie on the diagonal of opposite faces, these are also termed as diagonal planes of symmetry. Since there are 12 edges or six pairs of opposite edges in a cubic crystal, as much as six diagonal planes of symmetry are possible in a cubic crystal. One plane passing diagonally through the cubic crystal is shown in following figure (b).
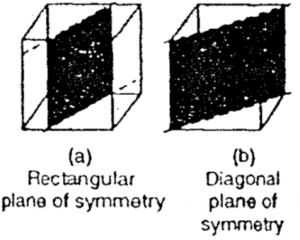
Thus in a cubic crystal, there are 3 rectangular planes of symmetry and 6 diagonal planes of symmetry, i.e. on the whole there are 3 + 6 = 9 planes of symmetry in a cubic crystal.
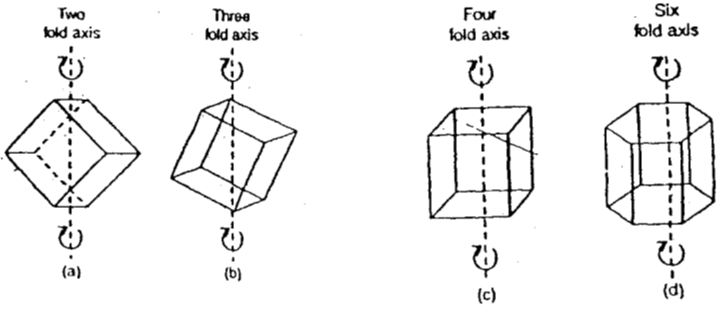
(B) Axis or line of symmetry:
It is an imaginary line (or axis) about which the crystal may be rotated so that it presents the same appearance more than once in a complete rotation through 360º. In a cubic crystal the axis of symmetry may be of three types depending upon the number of times the identical appearance occur during the course of a complete rotation of 360º.
(i) Axes of four fold symmetry: Imagine a line passing through the centres of two opposite faces of a cube. On rotating the cube about this line as axis, the self-coincidence (identical appearance) of the cube occurs four times during the course fo rotation through 360º, i.e. the original appearance is repeated as a result of rotation through 90º. Such an axis is said to be axis of four-fold symmetry or a tetrad axis. Now since there are six faces or three pairs of opposite faces in a cubic crystal, 3 such axes at right angles to each other are possible.
(ii) Axes of three fold symmetry: Imagine a line passing through the opposite corners of a cube along the body diagonal. On rotating the cube about this line as axis, the identical appearance of the cube occurs three times during the course of rotation through 360º, i.e. the original appearance is repeated as a result of rotation through 120º. Such an axis is said to be an axis of three-fold symmetry or a triad axis. Now since there are eight corners or four such body diagonally opposite pairs of corners in a cubic crystal, 4 such axes are possible.
(iii) Axis of two fold symmetry: Imagine a line passing through the centres of the two diagonally opposite edges of a cube. On rotating the cube about this line as axis, the identical appearance of the cube occurs two times during the course of rotation through 360º, i.e. the original appearance is repeated as a result of rotation through 180º. Such as axis is said to be an axis of two fold symmetry or a diad axis. Since there are twelve edges or six such diagonally opposite pairs of edges in a cubic crystal, 6 such axes are possible.
Thus in a cubic crystal, there are 3 axes of four-fold symmetry, 4 axes of three-fold symmetry and 6 axes of two-fold symmetry. Thus in all a cubic crystal has 3 + 4 + 6 = 13 axes of symmetry.
(iv) Axis of six fold symmetry: This axis of symmetry is possible in hexagonal crystals and not in cubic crystals. Imagine a line passing through the centres of two opposite hexagonal faces of a hexagonal crystal. On rotating the crystal (hexagonal) about this line as axis, the identical appearance of the hexagon occurs six times in the course of one complete rotation of 360º, i.e. the original appearance is repeated as a result of rotation through 60º. Such an axis is, therefore, known as an axis of six-fold symmetry or a hexad axis.
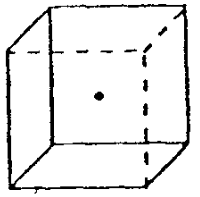
(C) Centre of symmetry:
It is such a point in the crystal that any line drawn through it intersects the surface of the crystal at equal distances on either side. A crystal may have one or more planes or axes of symmetry but it never has more than one centrel of symmetry which lies at the centre of the cube in following figure.
The total number of elements of symmetry in a cubic crystal are 23.
Plane of symmetry = 3 + 6 = 9
Axes of symmetry = 3 + 4 + 6 = 13
Centre of symmetry = 1
∴ Total number of elements of symmetry = 9 + 13 + 1 = 23
Contribution of different Lattice point in one Cubical unit cell :

Illustration: In a face centered cubic arrangement of A and B atoms whose A atoms are at the corner of the unit cell and B atoms at the face centres. One of the A atom Is missing from one corner in unit cell. The simplest formula of the compound is
(A) A7B3 (B) AB3 (C) A7B24 (D) A2B3

Wrong shortcode initialized





