WERNER’S THEORY OF COORDINATION COMPOUNDS

The geometries and properties of coordination compounds were first deduced by swiss chemist alfred werner in 1893, who was awarded the 1913 Noble prize in chemistry for his pioneering studies. This theory was put forward before the electron had been discovered by J.J. Thomson in 1896 and before the electronic theory of valency.

Postulates

The combining power of a metal atom is divided into two spheres of attraction: The inner or
the coordination sphere and the outer or the ionisation sphere.
The ionization sphere constitutes the entities which satisfy the primary valency of the metal.
The coordination sphere constitutes the entities which satisfy the secondary valency of the
metal. In a complex compound, coordination sphere is represented by square bracket [ ] and
the ionisation sphere is outside the coordination sphere as shown below:
Every metal has a fixed number of secondary valencies. The number of secondary valencies
equals the number of ligand atoms coordinated to the metal. (i.e., coordination number).
Primary valencies are satisfied by negative ions whereas secondary valencies may be satisfied
by either neutral molecules or negative ions or in rare cases by positive ions. According to modern concept of coordination compounds, the species satisfying the secondary
valency are called ligands.
The complex ion commonly exists as a positive ion.
The primary valency is equal to the number of charges on the complex ion.
Primary valencies are non directional whereas the secondary valencies are directional. The
secondary valency has a fixed orientation in space around the metal. The number of species satisfying the secondary valency gives a definite geometry to the coordination compound. The directional nature of secondary valencies makes possible the existence of stereoisomers
amongst inorganic complexes. Thus the complex, PtCl2·2NH3 exists in the geometrical
isomeric forms: cis and trans. Their structures may be represented as follows.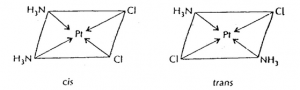

In a similar way, Werner studies a range of complexes which included [Pd(NH3)2Cl2]
The coordination number is 4 and the shape could be either tetrahedral or
square planar. Werner was able to prepare two different isomers for these complexes. A tetrahedral complex can only exist in one form, but a square planar complex can exist in two isomeric forms. This proved these complexes are square planar rather than tetrahedral.
When a coordination compound undergoes ionisation in aqueous solution, the species
satisfying the primary valency can be obtained in their free state whereas the species satisfying
the secondary valency can not be obtained in free state.

Explanation of cobalt amines on the basis of Werner’s theory.

The Werner’s postulates helped to explain the structures of various cobalt amines. For ex- ample to explain the bonding in CoCl₃6NH₃ complex on the basis of postulates of Werner’s theory.

1. CuCl₃.6NH₃

Cobalt has primary valency (oxidation state) of three and secondary valency (coordination number) six. As a convention secondary valencies are represented by solid lines (–) and primary valencies are shown by dotted line (…..). In the complex, all the six secondary valencies are occupied by six NH₃ molecules. The Cl^– ions are bonded to Co by three pri- mary valencies. These chloride ions are ionisable and, therefore, can be precipitated on the addition of silver nitrate. The central metal ion and the neutral molecules or ions (ligands) satisfying secondary valencies are written in a square bracket while writing the formula of the complex compound. Thus, the complex may be formulated as [Co(NH₃)₆]Cl₃ and may be represented as shown in Fig. 1. The primary valencies, as already discussed, are ionizable and, therefore, all the chloride ions would get precipitated on the addition of silver nitrate. The ionisation of the complex is written as:

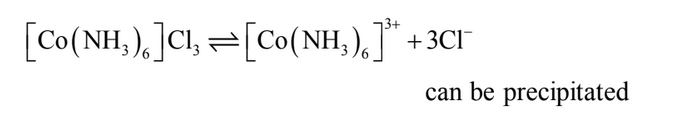
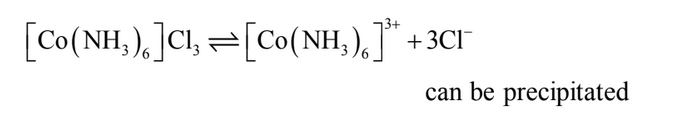
2. CoCl₃.5NH₃

In this compound, the coordination number of cobalt remains 6 but now five positions are occupied by NH₃ molecules and the sixth position by one of the chloride ions. This chloride ion has a dual character as it satisfied secondary as well as a primary valency. This is indi- cated by a full line as well as a dotted line, as shown in Fig. 2. The two Cl– ions satisfy the remaining two primary valencies of cobalt. This satisfies 6 secondary and 3 primary valen- cies of cobalt. However, on ionisation, only two 2Cl– ions will be precipitated because one Cl– ions, which also satisfies secondary valency, will not be precipitated.

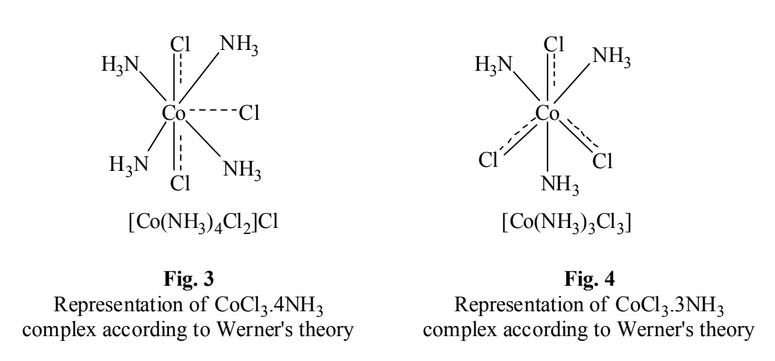
3. CoCl₃.4NH₃ Complex

In the compound CoCl₃.4NH₃ , two chloride ions exhibit dual character of satisfying both primary and secondary valencies. This is show in Fig. 3. It will give precipitate with silver nitrate corresponding to only one Cl– ion and the number of ions in this case is 2. It may be formulated as [Co(NH₃)Cl₂]Cl ionises as:

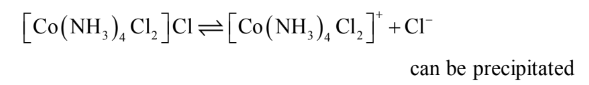
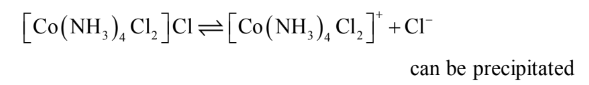
4. CoCl₃.3NH₃ Complex

In this compound, three chloride ions satisfy primary and secondary valencies as shown in Fig. 4. It is clear from the figure that all the chloride ions are non-ionizable and will not be precipitated by the addition of AgNO₃ . Therefore, the complex behaves as neutral non-con- ducting molecule. It may be formulated as [Co(NH₃)₃Cl₃] and does not ionise:

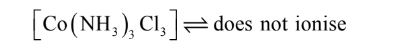
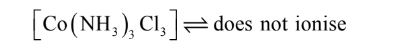
The structures of coordination compounds of cobalt chloride and ammonia are summed up in Table.

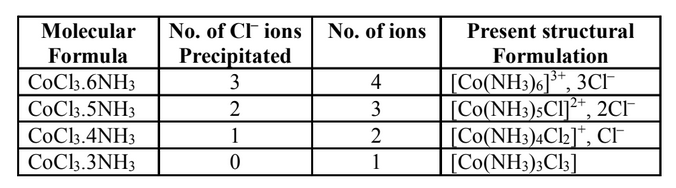Table: Structure of some coordination compounds of CoCl₃ and NH₃ Werner also explained successfully the structures of amines of Pt4+, In all these complexes, platinum exhibits a primary valency of four and secondary valency of six. The structures of these complexes are given in Table.

Table: Structure of some coordination compound of PtCl4 and NH3

Verification of Werner’s Theory

(1.) Conductivity Measurement
The molar conductivity of an ionic compound depends on:

The concentration of solute.
The no. of charges on the species which are formed on dissolution.

Molar conductivity relates to a 1 M solution and thus the concentration factor is removed. As the number of charges increases, the molar conductivity of the complexes also increases. The molar conductivity measurement of cobalt/ammonia/chlorine complexes suggest structures similar to Werner’s Theory.

(2) Cryoscopic Measurement The freezing point of a liquid is lowered when a non volatile chemical substance is dissolved in it. Cryoscopic measurements involve measuring how much the freezing point is lowered. The depression of freezing point obtained depends upon measurements that can be used to find if a molecule dissociates how may ions are formed. If a molecule dissociates into two ions it will give twice the expected depression for a single particle. If three ions are formed this will give three times the expected depression. Thus:

The number of particles formed from a complex molecule determines the size of the depression of freezing point. Note that the number of particles formed may be different from the total number of charges which can be obtained from conductivity measurements. The two types of information can be used together to establish the structure. Molar conductivities and cryscopic measurements for chromium (III) complexes involving ammonia molecules and chloride ions, for example, helps in demarcating the coordination sphere from ionization sphere.

(3) Dipole moment Measurement
Dipole moment measurement may also give structural information but only for non-ionic complexes. For example: The complex Pt(NH₃)₂Cl₂ is square planar and can exist as cis or trans forms. The dipole moment from the various metal-ligand bonds cancel out in the trans forms. However, a finite dipole moment is given by the cis forms.

Illustration: Using the following information, establish the correct structure of the complexes.

Solution: On the basis of molar conductivity and cryscopic measurement data, the structure of-

Illustration: One mole of a pink solid (X), having empirical formula, CoCl3 ·5NH3 ·H2O gives three moles of silver chloride on treatment with excess of silver nitrate solution. On heating X loses a molecules of water to give a purple solid (Y) which has the same NH3 : Cl : ratio. Deduce the structures of X and Y.

Solution:

Wrong shortcode initialized

WERNER’S THEORY OF COORDINATION COMPOUNDS